the drawing shows a compass and straightedge construction of

Smarsh28965 June 29, 2022 a , and , compass , drawing Comment

In order to show that an equilateral triangle actually existed Euclid had to develop an algorithm to construct an equilateral triangle. A congruent angle C.

How To Construct Draw An Equilateral Triangle With Compass And Straightedge Or Ruler Hs Geometry Technical Drawing Triangle

Then draw a ray from the vertex which will be one of the legs of the new angle.

. It should be pointed out that the compasses that they used were collapsibleThat is you could open the compass and draw an arc but immediately after you removed a point of the compass from. Then construct a circle centered at B on IBCI and a circle centered at C on CBI intersecting at point D. Draw an arc between point A and point B.

Then AD bisects Angle BAC. The new line formed will bisect the angle. Straightedge and compass construction also known as ruler-and-compass construction is drawing of lengths angles or shapes using only a ruler and compass.

Student 1Fix the compass at M and adjust its width to point L. Perpendicular bisector lublana lublana Answer. Basic Constructions and Limitations In Euclids Elements Book 1 the very first proposition states To construct an equilateral triangle on a given finite straight-line Heiberg Fitzpatrick Euclid pg 8 This proposition is saying that it is possible to construct an equilateral triangle.

For example there are only 32 regular polygons with an un even number of sides which are known to be constructible. Z t The drawing shows a compass and straightedge construction of - P a line segment congruent to a given line segment the bisector of a given angle H an angle congruent to a given angle the bisector of a line segment Previous Next See the Expert Answer Click to see the answer prepared by our experts SEE THE ANSWER Related Questions Math. In the branch of mathematics known as Euclidean geometry the PonceletSteiner theorem is one of several results concerning compass and straightedge constructions with additional restrictions imposed.

This construction is shown by option D. Compass and straightedge constructions are of historical significance. Draw an arc above point A.

Draw a line segment from P that passes. Draw a line by joining vertex of an angle and the point of intersection of two arcs. What is the next step in the construction.

Ruler and a pencil. Place the compass needle on M and keeping the compass width the same draw two arcs that intersect. 465 43 votes.

It works because the compass width is not changed between drawing each. Answer choices Draw an arc above point A Measure the length of segment AB Draw an arc between point A and point B Measure half the length of. Label these points B and C.

Measure the length of segment AB. Straightedge and compass construction also known as ruler-and-compass construction is drawing of lengths angles or shapes using only a ruler and compass. Then draw an arc from the point where the first arc from vertex intersects the lines.

Geometry questions and answers. Draw an arc between point A and point B. Start with angle BAC and construct a circle centered at A on IABI and let it intersect the ray AC at the point C.

The ancient Greeks are the most well-known civilization for investigating these constructions on an elementary level. Answer choices the bisector of a given angle a perpendicular to a given line at a point on the line a perpendicular to a given line from a point NOT on the line an angle congruent to a given angle Question 2 60 seconds Q. Answer to Solved G.

To bisect an angle we need to draw an arc from vertex which intersects all the two sides. Draw an arc above point A. A perpendicular bisector D.

When copying line segment AB using a straight edge and a compass the compass should be used to. Many old problems in geometry ask whether certain operations or quantities can be constructed in this fashion. The compass and straightedge is more important in constructing geometric structures than other drawing tools such as rulers and protractors.

Construction in Geometry means to draw shapes angles or lines accurately. A congruent line segment 2 See answers crystalhn209 crystalhn209 C. The given diagram is what kind of construction.

Because steps taken with a compass and straightedge cannot be seen at first glance and this situation become a problem for students. Option C a perpendicular bisector. Using A as a center we draw an arc of a circle intersecting the two sides of the angle.

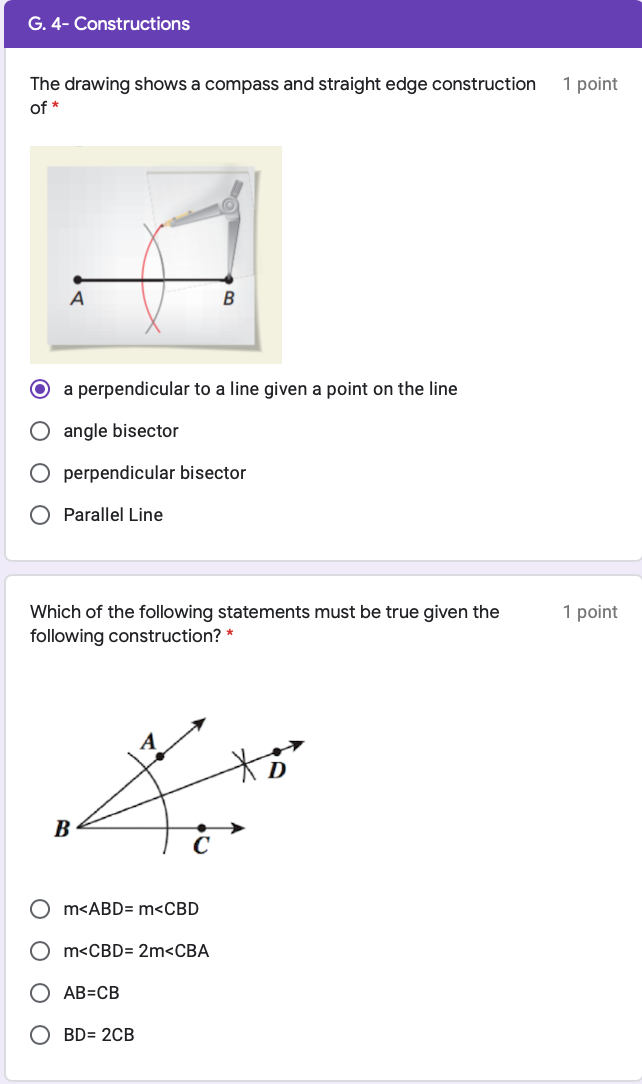
4- Constructions 1 point The drawing shows a compass and straight edge construction of А B a perpendicular to a line given a point on the line O angle bisector O perpendicular bisector O Parallel Line 1 point Which of the following statements must be true. This figure represents a step in a compass-and-straightedge construction. Straightedge and compass constructions In classical geometry the tools of a straightedge a ruler without markings and a compass which makes circles are used to construct new shapes out of old ones.

This is the pure form of geometric construction. The drawing shows a compass and straight edge construction ofwhat. An angle bisector B.

This result states that whatever can be constructed by straightedge and compass together can be constructed by straightedge alone provided that a single circle and its centre. These constructions use only compass straightedge ie. For the duration of this paper we will arm ourselves.

Construct an equilateral triangle on a given nite straight line. The figure below shows a partially completed set of steps to construct a rhombus PQRS. Without changing the width of the compass move the compass to N and draw a small arc on the big arc.

Label the point of intersection of the two arcs as T. To copy an angle using only a compass and a straightedge begin by marking the vertex of the new angle. When copying line segment AB using a straight edge and a compass the compass should be used to.

4- Constructions 1 point The drawing shows a. The segments and are congruent these are both radii of the circle. The idealized ruler known as a straightedge is assumed to be infinite in length and has no markings on it and only one edgeThe compass is assumed to.

Compass-and-straightedge construction also known as ruler-and-compass construction or classical construction is the construction of lengths angles and other geometric figures using only an idealized ruler and compass. He assumes that it is possible to. Draw an arc above point A.

Ruler and compass Some things cannot be drawn this way. Draw the circle with center B and radius r BC.

Art Using Basic Geometry Constructions With Compass And Straightedge Math Art Geometry Projects Art Lessons Elementary

5 The Drawing Shows A 1 Point Compass And Straigh Gauthmath

How To Construct A 90 Degree Angle With Compass And Straightedge Or Ruler Math Open Reference Geometric Construction Technical Drawing Degree Angle

How To Construct A 60 Degree Angle With Compass And Straightedge Or Ruler Math Open Reference Geometry Angles Geometric Construction Geometry Constructions